数据结构二分查找

对顺序查找法、二分查找法和分块查找做系统学习。用的书是严老师(严薇敏)的C语言版，使用scala重新编写了一下。语法稍微不同思路是一样的。

二分查找实现与演算

二分查找的一个前提是必须保证序列有序，假如一个无序的序列想要使用二分查找，实际上速度并不一定比顺序查找要快，因为在进行二分查找之前，需要经过排序，而排序往往消耗的时间页是巨大的。

def binary(arr : Array[Int],elem : Int) : Int = {
    var low = 1;
    var hight = arr.length;
    while (low <= hight){
        var mid = ( low + hight ) / 2
        if(arr(mid) == elem){
            return mid
        }else if(arr(mid) > elem){
            hight = mid - 1
        }else{
            low = mid - 1
        }
    }
    return 0
}

这个算法需要注意的是，循环执行的条件是low<=hight,而不是low<hight,因为在low<hight时，查找区间还有最后一个结点，还要进行一步比较。

算法演算过程如下图:

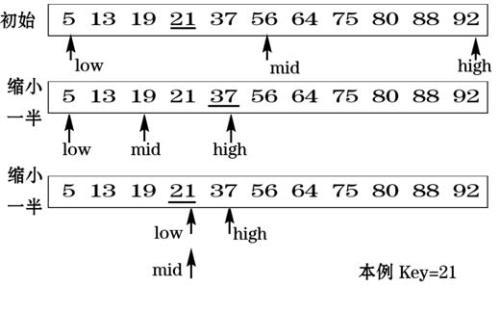
假如key=21可以看到第一次先和56比，发现key<57，接着和19比,发现key>19以此类推最终找到21。

---

时间复杂度计算

其实我们可以把查找的过程映射成决策树，事情就会变得更加有趣。

首先我们需要知道什么是满二叉数,像下图中的(a)

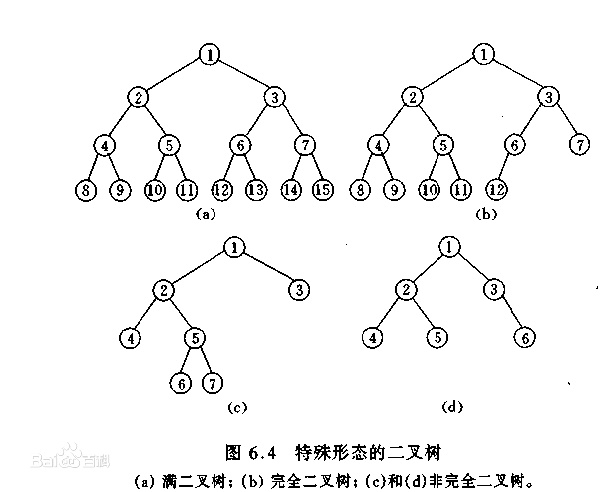
我们遵循一个规律树的左子树都比根节点小，树的右子树都比根大。遵循这个策略有序序列映射后就会变成下面的样子

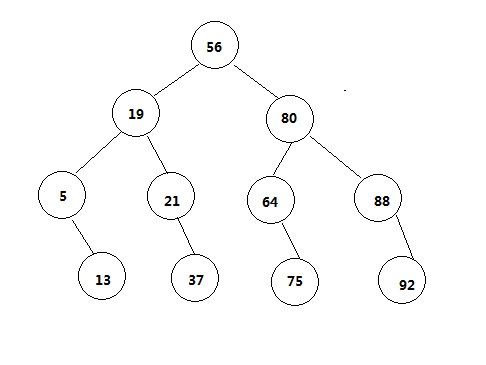
对照这树，我们可以发现，第一层的我们最多只用比一次就可以找到对应的值，第二层的节点想要找到得比两次，第三层的节点想要找到得比三次,第四层的节点想要找到就得比四次。因为我们遵循着左小右大的原则,假设每个节点找到的概率都想等，那么平均寻找长度我们就可以计算出来

$$ALS=\frac{1}{11} \left( 1+22+34+4*4 \right) = 3$$

好了!11个节点的有序序列利用二分查找法的平均寻找长度我们算出来是3。那么思考一个问题：对于n个结点的有序序列，如何求出它的平均寻找长度？

对于这个问题我们需要一些基础知识，满二叉数的结点数总数 $$\left( s \right) $$ 与深度$$\left( h \right) $$ 存在这这样的公式

$$s=2^h-1$$

满二叉数的第n层的节点总数 $$\left( n \right) $$ 与深度$$\left( h \right) $$ 存在这这样的公式

$$n=2^{h-1}$$

上面的公式还可以转换成这样的形式

$$h = \lfloor\log_2 n\rfloor + 1$$

对于n个节点的有序序列，映射到满二叉树上以后，第一层的我们最多只用比一次就可以找到对应的值，第二层得比两次,第三层得比三次…第n层就得比$$h\cdot2^{h-1}$$次(提示:等比数列通向式)，假设每个节点找到的概率都想等，则平均寻找长度为

$$ALS=\frac{1}{n}\left(1+22+33+ \cdots + \left( h-1 \right) * 2^{h-2} + h * 2^{h-1} \right)$$

继续推导

$$ALS=\frac{1}{n} \sum_{j=1}^h\ j\cdot2^{j-1}$$

继续推导

$$ALS=\frac{n+1}{n} \log_2 \left(n+1\right) - 1$$

当n较大时，有下面近似值

$$ALS=\log_2 \left(n+1\right) - 1$$

则二分查找的时间复杂度为$$\omicron \left( \log_2 n \right)$$

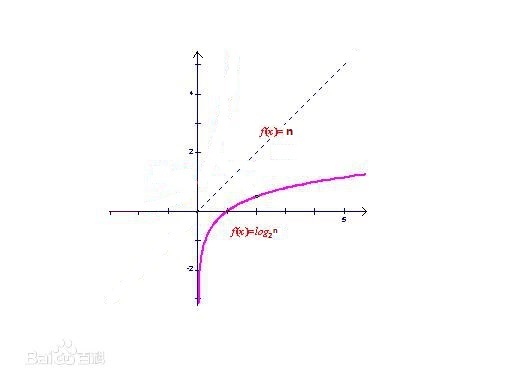
借助下面的图形可以看出二分查找的效率要比顺序查找的效率高的多，当n>0并趋向于无穷时，效果会越来越明显。

分块查找见下一节