数据结构分块查找

分块查找是顺序查找和二分查找的一个折中选择。它由索引表和块*n组成

遵循这样的原则：索引表中存放这块内最大key和块的内存起始地址,并且索引表内key由小到大排列;每个块内的key不必有序。

块的大小决定这查询的效率。随意取会影响查询速度，后面会介绍块的最优大小如何算得。

分块查找的结构图如下图所示：

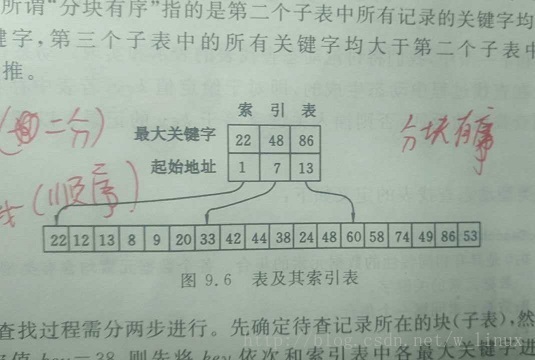
查询的过程分为两步，先通过索引表确定key所在块，由于索引表是有序的并且数据量不会很大、所以使用顺序或者二分查找都可以。确定到块后由于块内无序，所以只能使用顺序查找。那么求得的总的平均查找长度为

$$ASL_{bs} = L_b + L_w$$

其中,$$L_b$$为查找索引表确定所在块的平均查找长度，$$L_w$$为在块中查找元素的平均查找长度

一般情况下，为进行分块查找，可以将长度为n的表平均分为b块，每块含s个记录，则 $$b=\lceil\frac{n}{s}\rceil$$,又假定表中每个记录的查找概率相等，则每个块查找的概率为$$\frac{1}{b}$$,块中每个记录的查找概率为 $$\frac{1}{s}$$

若用顺序查找确认所在块，则分块查找的平均查找长度为：

$$ASL_{bs} = L_b + L_w = \frac{1}{b}\sum_{j=1}^b j + \frac{1}{s}\sum_{i=1}^s i = \frac{b+1}{2} + \frac{s+1}{2}$$

继续推导

$$ASL_{bs} = \frac{1}{2}\left(\frac{n}{s}+s\right)+1$$

此时的平均查找长度不仅和表长n有关，而且和每一块中的记录个数也有关，在给定n的前提下， s是可以选择的，容易证明，当s是$$\sqrt{ n }$$ 时，$$ASL_{bs}$$取最小值$$\sqrt{ n }+1$$，这个比值比顺序查找虽然快但不及二分查找。