一元线性回归分析(R语言)

回归分析就是利用样本(已知数据),产生拟合方程,根据回归结果，得出各个因变量对目标变量产生的影响，还可以(对未知数据)进行预测。

计算实例

下面参考薛毅的书例6.5进行阐述一元回归模型的计算过程。

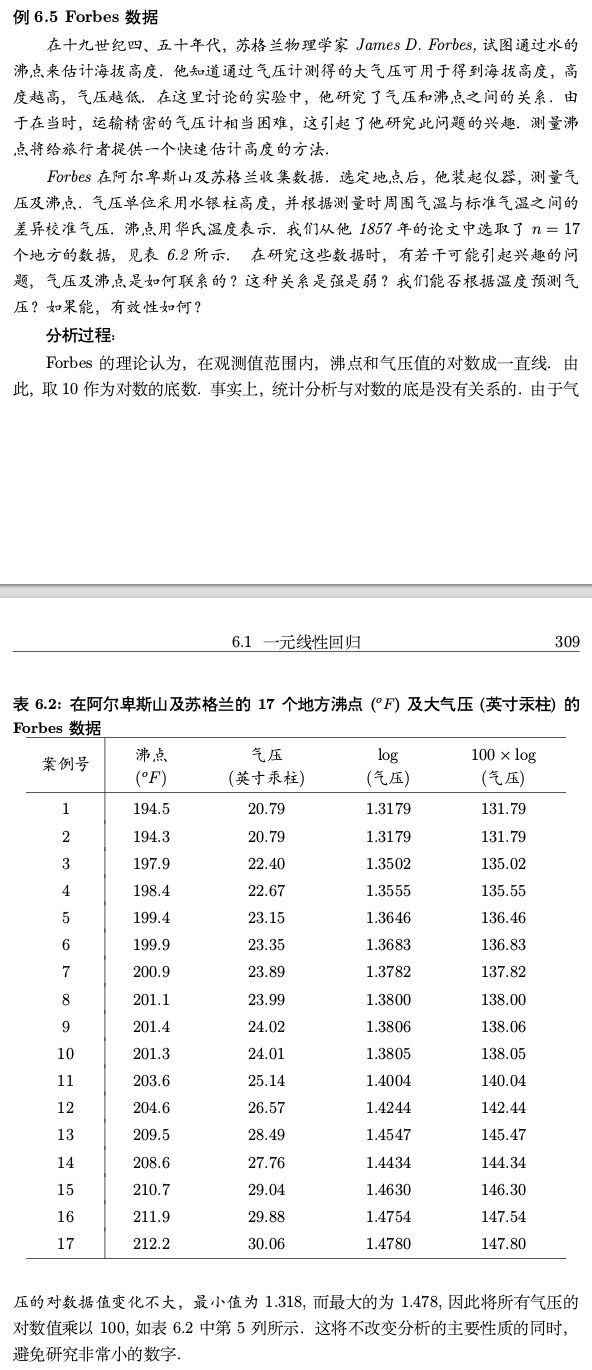
画出散点图

我们利用R画出散点图

# 读取数据，生成矩阵
X <- matrix(c(
194.5, 20.79, 1.3179, 131.79,
194.3, 20.79, 1.3179, 131.79,
197.9, 22.40, 1.3502, 135.02,
198.4, 22.67, 1.3555, 135.55,
199.4, 23.15, 1.3646, 136.46,
199.9, 23.35, 1.3683, 136.83,
200.9, 23.89, 1.3782, 137.82,
201.1, 23.99, 1.3800, 138.00,
201.4, 24.02, 1.3806, 138.06,
201.3, 24.01, 1.3805, 138.05,
203.6, 25.14, 1.4004, 140.04,
204.6, 26.57, 1.4244, 142.44,
209.5, 28.49, 1.4547, 145.47,
208.6, 27.76, 1.4434, 144.34,
210.7, 29.04, 1.4630, 146.30,
211.9, 29.88, 1.4754, 147.54,
212.2, 30.06, 1.4780, 147.80),
ncol=4, byrow=T,
dimnames = list(1:17, c("F", "h", "log", "log100")));
forbes<-as.data.frame(X);
# 将F列映射在x轴和log100列映射在y轴描绘出散点图
plot(forbes$F,forbes$log100);

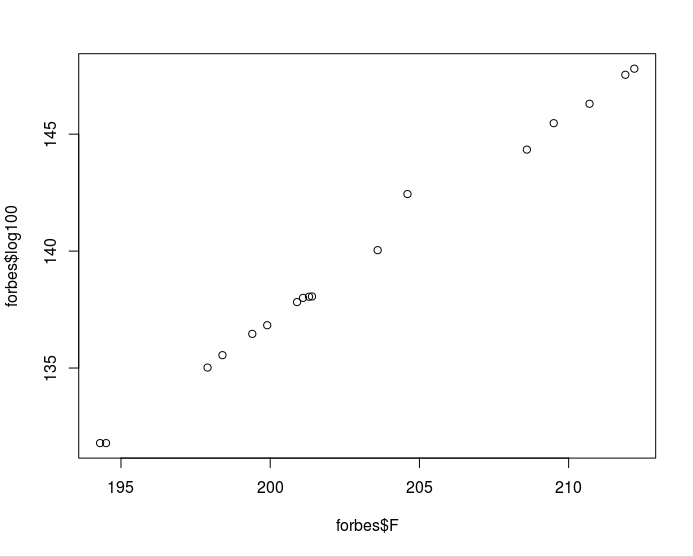
可以大致看出图形乘线性增长趋势，做回归分析，设线性回归方程为:

$$y=ax+b$$

根据线性回归方程，在R中描绘出log100关于F的函数

lm.sol<-lm(log100~F,data=forbes);
# 画出回归方程
abline(lm.sol);

R是怎么画出这条线的？

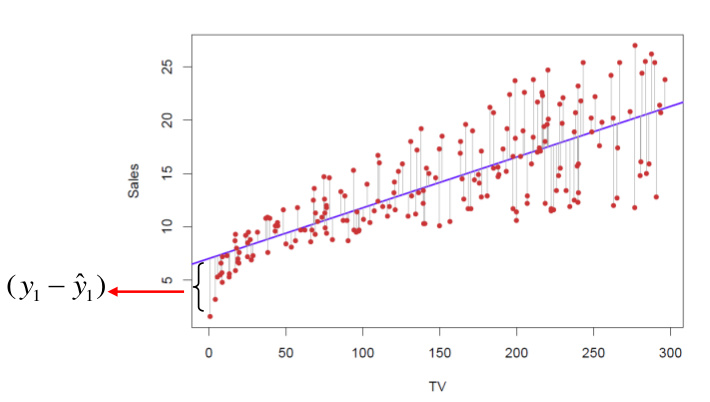
首先做样本点到一元回归方程且平行与Y轴的一条线段，并求得每个样本点的误差值,这样问题就可以转换为怎么画这条直线才能使得残差平方和最小

什么是残差平方和,对于上图中每个误差值的绝对值的总和称为残差和，由于带着绝对值求解不太方便，所以对误差值的平方后求和，即为残差平方和

$$f\left(a,b\right)=\sum_{i=1}^{n}{\left(Y_i - \left(\ aX_i + b \right)\right)^2}$$

对于函数的极值问题，利用高等数学中偏导数定理，即$$\frac{\delta f}{\delta a}=0$$和$$\frac{\delta f}{\delta b}=0$$。下面为证明过程,由于公式太难打这边就插图了：

最终求得a和b的值。有了这个公式，对于本例子，我们就可以算出拟合直线具体是什么。分别求出公式中的各种平均数，然后带入即可，最后算出a=0.89546，b=-42.13087

最终的回归拟合直线为

$$Y=-42.13087 + 0.89546X$$

评价回归线拟合程度的好坏

可以使用R里面的**summary()**函数解决这个问题。

> summary(lm.sol)

Call:
lm(formula = log100 ~ F, data = forbes)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.32261 -0.14530 -0.06750  0.02111  1.35924 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -42.13087    3.33895  -12.62 2.17e-09 ***
F             0.89546    0.01645   54.45  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 0.3789 on 15 degrees of freedom
Multiple R-squared:  0.995,	Adjusted R-squared:  0.9946 
F-statistic:  2965 on 1 and 15 DF,  p-value: < 2.2e-16

参数详述

Residuals: 列出了残差的最小值、下四分为数、中位数、上四分为数、最大值

Coefficients : -42.13087表示的是截距、0.89546表示的是斜率,推算的系数的标准差,t值,P-值(结合Signif做显著性检验)

Signif:显著性标记,三颗表示极度显著,二颗表示高度显著,一颗*表示显著,圆点表示不太显著,没有记号表示不显著

Residual standard error : 残差标准查

Multiple R-squared : 相关系数平方

F-statistic: F检验值

推荐一篇不错的blog回归分析法&一元线性回归操作和解释