B-树

B+树，称为B加树；那么对于B-树，谁要是读成B减树，那就太丢人了咯，它虽然带着减号，但是要读成B树。

B+树和B-树是一种基础的数据结构，做为开发人员一定要掌握。

什么是B-树

首先大家都知道数据库有索引，索引被映射成二叉索引树，被存在于磁盘之上。那么下面我们来看看为啥数据库要使用B-树？换二叉搜索树行不行？

从算法逻辑上来讲，二叉搜索树的查找速度和比较次数都是最小的，但是数据库的实现并没有用二叉搜索树，而是用了B-树和B+树，下面来说一下里面的门道。

数据库操作数据要进行频繁的“磁盘IO”，因此在设计之初要充分考虑到如何优化磁盘IO造成的读写效率问题。数据库索引存于磁盘之上，当数据量比较大的时候，索引的大小可能有几个G甚至更多。当利用索引查询的时候，肯定不能将全部都加载到内存，能做的只有逐一加载每个磁盘页，这里的磁盘页对应索引树的节点。

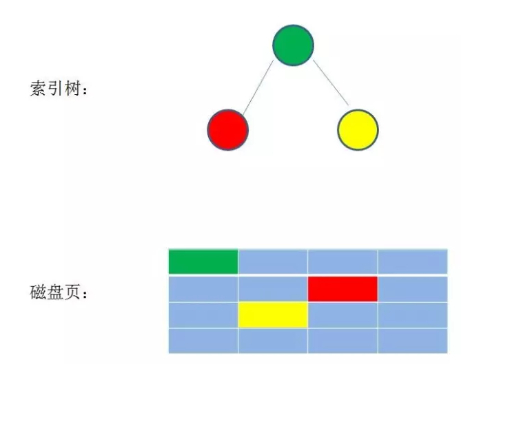
探究一下如果索引树使用二叉搜索树实现，会是一种什么样的情况，假设树的高度是4，查找的值是10

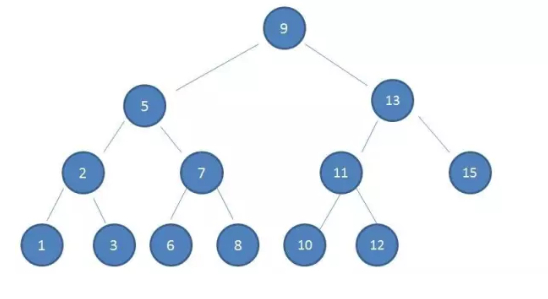
第1次IO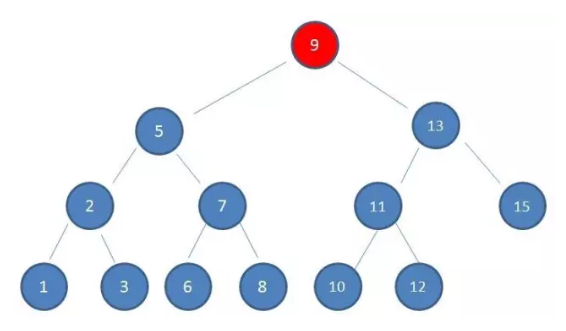

第2次IO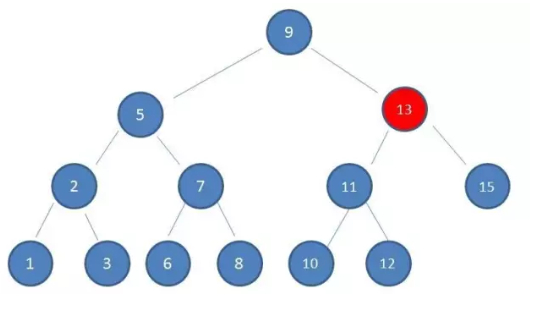

第3次IO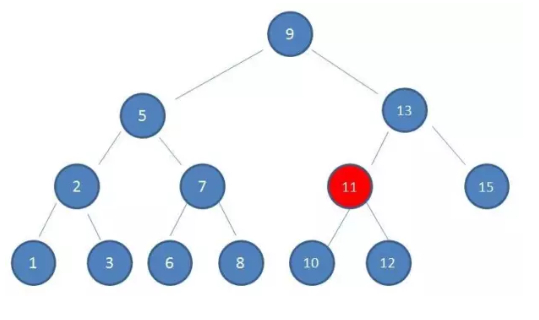

第4次IO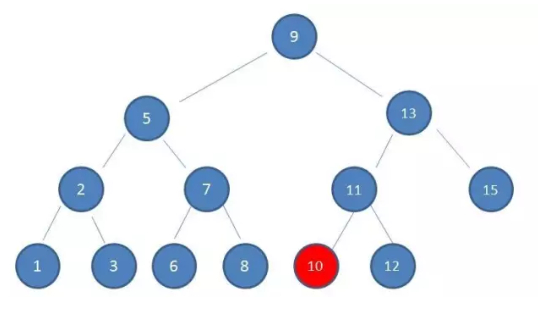

查找了4次命中结果，因此磁盘IO的次数是由树的高度决定。为了减少磁盘IO次数，下面使用B-树来将二叉搜索树进行“瘦身”，以此来减少IO次数！

下面来具体介绍一下B-树（Balance Tree），一个m阶的B树具有如下几个特征：

根结点至少有两个子女。
每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
所有的叶子结点都位于同一层。
每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

以3阶 B-树为例，来认识一下B-树的具体结构。树中的具体元素和上图二叉搜索树节点一样。

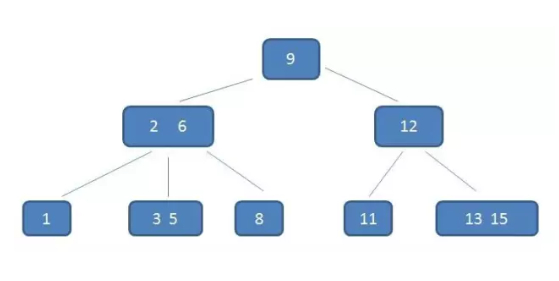
这棵树中，重点看（2,6）节点，该节点有两个元素2和6，又有三个孩子1，（3,5），8；其中1小于元素2，（3,5）在元素2,6之间，8大于（3,5），符合B-树的几个特征。

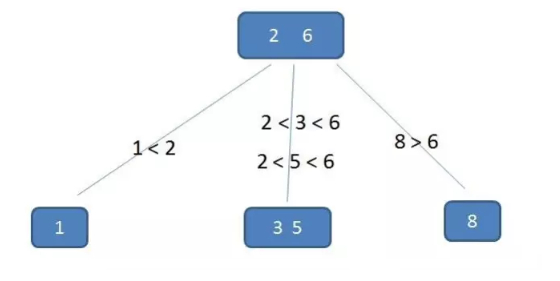
B-树的查找

假如要查的值为5

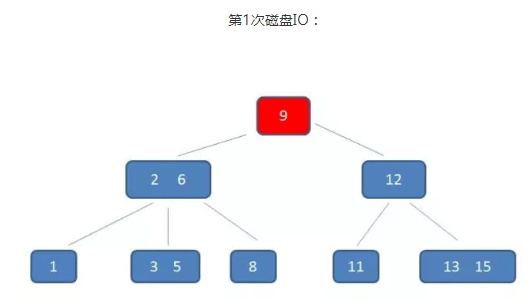
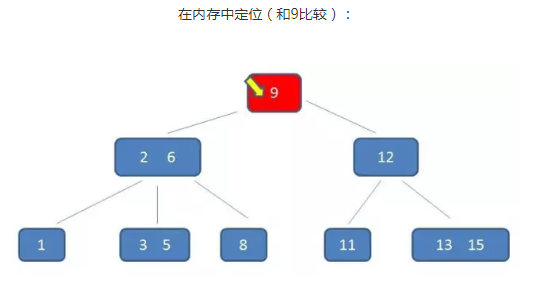
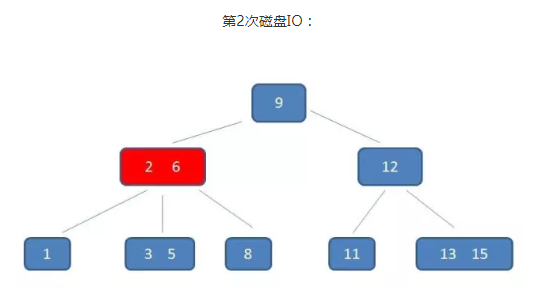
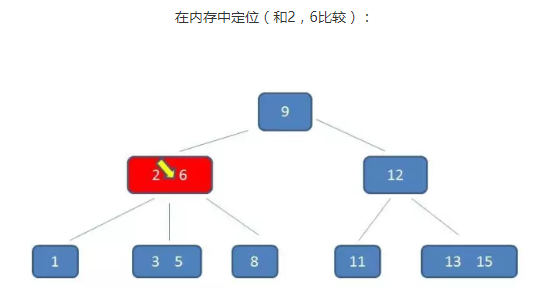
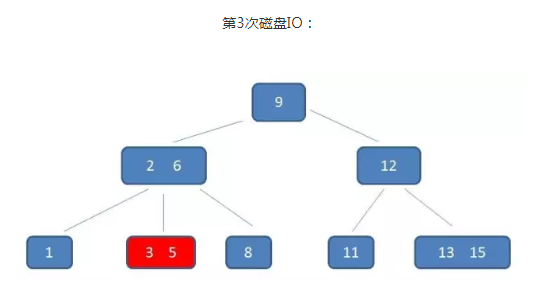
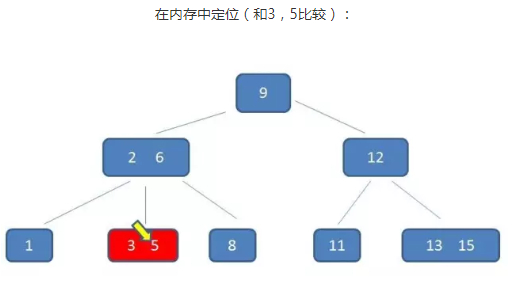
通过整个流程可以看出 B-树 在查询中比较次数其实不比二叉树少，尤其当单一节点中的元素数量很多时。

可是相比磁盘IO的速度，内存中比较耗时几乎可以忽略，所以只要树的高度足够低，IO次数足够少，就可以提升查找性能。

相比之下节点内部元素多一些也没有关系，仅仅是多了几次内存交互，只要不超过磁盘页的大小即可，这也是B-树的重要优势之一。

B-树的插入

B-树插入新节点过程比较复杂，而且分很多种情况。这边举一个最典型例子，加入我们要插入的值是4

自顶向下查找4的节点位置，发现4应当插入到节点元素3，5之间。

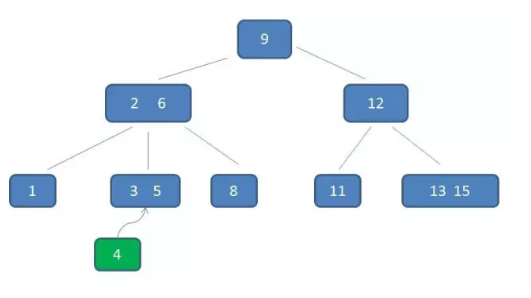
节点3，5已经是两元素节点，无法再增加。父亲节点 2， 6 也是两元素节点，也无法再增加。根节点9是单元素节点，可以升级为两元素节点。于是拆分节点3，5与节点2，6，让根节点9升级为两元素节点4，9。节点6独立为根节点的第二个孩子。

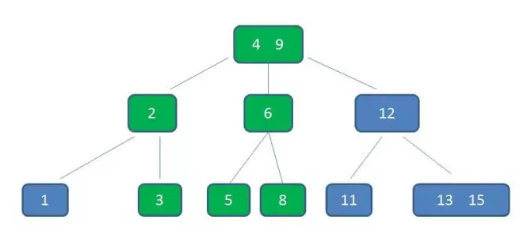
B-树的删除

下面演示一下B-树删除元素11的过程

自顶向下查找元素11的节点位置。

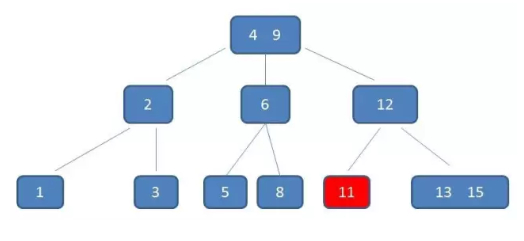
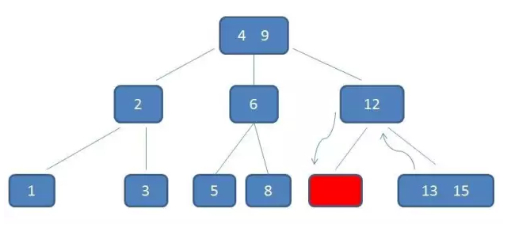
删除11后，节点12只有一个孩子，不符合B树规范。因此找出12,13,15三个节点的中位数13，取代节点12，而节点12自身下移成为第一个孩子。（这个过程称为左旋）

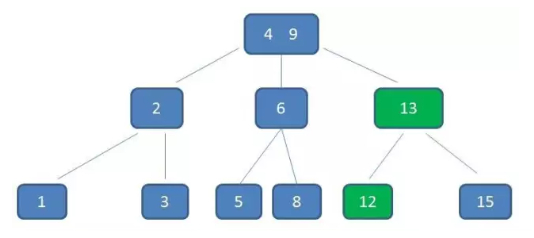
小结

B-树主要应用于文件系统以及部分数据库索引，比如MongoDB。

大部分关系型数据库，比如myslq，则使用B+树作为索引。