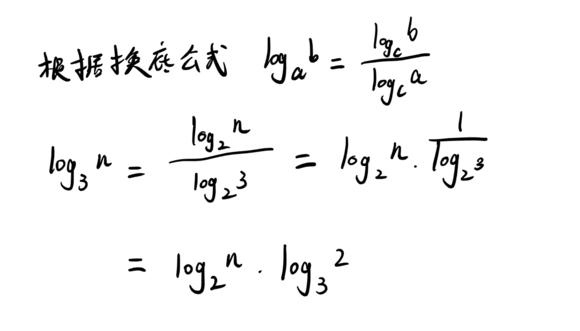时间空间复杂度
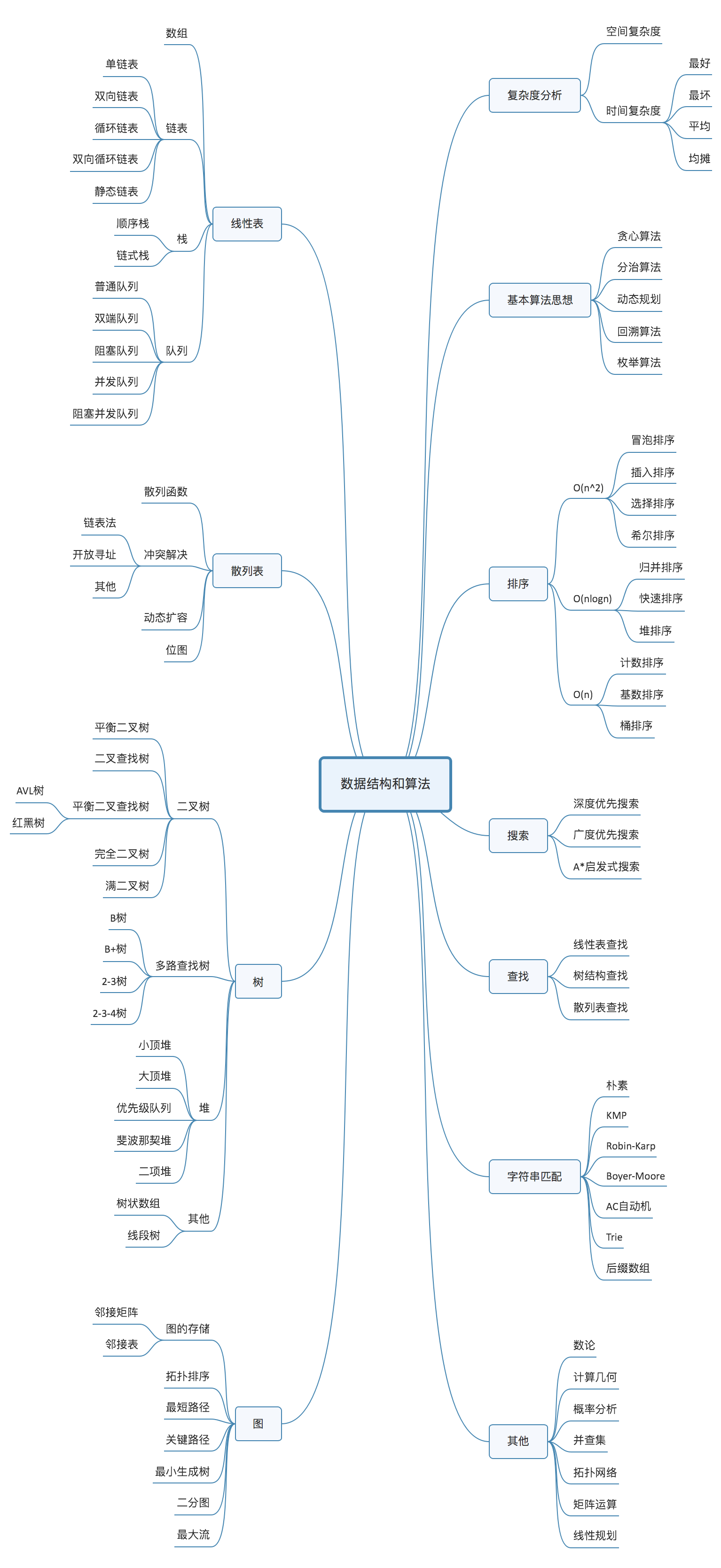
算法与数据结构相辅相成,谁也离不开谁,学算法和数据结构可以说让我很痛苦,当然对于聪明的你来说,这可能不是什么难事,哈哈哈。这下面的图是算法的整个知识体系图,通过让我们对整个算法体系有个初步了解。
我总结了20个最常用的、最基础数据结构与算法,他们分别是10个数据结构:数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie树;10个算法:递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法。
如果想学好算法,就得掌握怎么分析代码的性能。业界中常用时间复杂度和空间复杂度来坑量,类似O(1)、O(n)、O(n^2)等。如果说不会求时间和空间复杂度,那只能说你和算法无缘了!下面我们来理理到底应该怎么算,另外算这些东西不需要什么很高深的数学,只需要高中数学知识就足够了。下面会牵扯到一些对数运算,如果你忘了,建议你回去复习一下。
大O复杂度表示法
这里有段非常简单的代码,求1,2,3…n的累加和。现在,我就带你一块来估算一下这段代码的执行时间。
1 | |
假设每行代码执行的时间都一样,为unit_time。在这个假设的基础之上,这段代码的总执行时间是多少呢?
第2、3行代码分别需要1个unit_time的执行时间,第4、5行都运行了n遍,所以需要2n * unit_time的执行时间,所以这段代码总的执行时间就是(2n+2) * unit_time。可以看出来,所有代码的执行时间T(n)与每行代码的执行次数成正比
按照这个分析思路,我们再来看这段代码。
1 | |
我们依旧假设每个语句的执行时间是unit_time。那这段代码的总执行时间T(n)是多少呢?
第2、3、4行代码,每行都需要1个unit_time的执行时间,第5、6行代码循环执行了n遍,需要2n * unit_time的执行时间,第7、8行代码循环执行了n^2 遍,所以需要 2n^2 * unit_time的执行时间。所以,整段代码总的执行时间T(n) = (2n ^ 2 + 2n+3)*unit_time
尽管我们不知道unit_time的具体值,但是通过这两段代码执行时间的推导过程,我们可以得到一个非常重要的规律,那就是,所有代码的执行时间T(n)与每行代码的执行次数n成正比。
我们可以把这个规律总结成一个公式。注意,大O就要登场了!
我来具体解释一下这个公式。其中,T(n)我们已经讲过了,它表示代码执行的时间;n表示数据规模的大小;f(n)表示每行代码执行的次数总和。因为这是一个公式,所以用f(n)来表示。公式中的O,表示代码的执行时间T(n)与f(n)表达式成正比。
所以,第一个例子中的T(n) = O(2n+2),第二个例子中的T(n) = O(2n^2+2n+3)。这就是大O时间复杂度表示法。大O时间复杂度实际上并不具体表示代码真正的执行时间,而是表示代码执行时间随数据规模增长的变化趋势,所以,也叫作渐进时间复杂度(asymptotic time complexity),简称时间复杂度。
当n很大时,你可以把它想象成10000、100000。而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了,如果用大O表示法表示刚讲的那两段代码的时间复杂度,就可以记为:T(n) = O(n); T(n) = O(n^2)。
时间复杂度分析
前面介绍了大O时间复杂度的由来和表示方法。现在我们来看下,如何分析一段代码的时间复杂度?我这儿有三个比较实用的方法可以分享给你。
1.只关注循环执行次数最多的一段代码
我刚才说了,大O这种复杂度表示方法只是表示一种变化趋势。我们通常会忽略掉公式中的常量、低阶、系数,只需要记录一个最大阶的量级就可以了。所以,我们在分析一个算法、一段代码的时间复杂度的时候,也只关注循环执行次数最多的那一段代码就可以了。这段核心代码执行次数的n的量级,就是整段要分析代码的时间复杂度。
为了便于你理解,我还拿前面的例子来说明。
1 | |
其中第2、3行代码都是常量级的执行时间,与n的大小无关,所以对于复杂度并没有影响。循环执行次数最多的是第4、5行代码,所以这块代码要重点分析。前面我们也讲过,这两行代码被执行了n次,所以总的时间复杂度就是O(n)。
2.加法法则:总复杂度等于量级最大的那段代码的复杂度
我这里还有一段代码。你可以先试着分析一下,然后再往下看跟我的分析思路是否一样
1 | |
这个代码分为三部分,分别是求sum_1、sum_2、sum_3。我们可以分别分析每一部分的时间复杂度,然后把它们放到一块儿,再取一个量级最大的作为整段代码的复杂度。
第一段的时间复杂度是多少呢?这段代码循环执行了100次,所以是一个常量的执行时间,跟n的规模无关。
这里我要再强调一下,即便这段代码循环10000次、100000次,只要是一个已知的数,跟n无关,照样也是常量级的执行时间。当n无限大的时候,就可以忽略。尽管对代码的执行时间会有很大影响,但是回到时间复杂度的概念来说,它表示的是一个算法执行效率与数据规模增长的变化趋势,所以不管常量的执行时间多大,我们都可以忽略掉。因为它本身对增长趋势并没有影响。
那第二段代码和第三段代码的时间复杂度是多少呢?答案是O(n)和O(n^2),你应该能容易就分析出来,我就不啰嗦了。
综合这三段代码的时间复杂度,我们取其中最大的量级。所以,整段代码的时间复杂度就为O(n^2)。也就是说:总的时间复杂度就等于量级最大的那段代码的时间复杂度。那我们将这个规律抽象成公式就是:
如果T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n)+T2(n)=max(O(f(n)), O(g(n))) =O(max(f(n), g(n))).
3.乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
我刚讲了一个复杂度分析中的加法法则,这儿还有一个乘法法则。类比一下,你应该能“猜到”公式是什么样子的吧?
如果T1(n)=O(f(n)),T2(n)=O(g(n));那么T(n)=T1(n) * T2(n) = O(f(n)) * O(g(n)) = O(f(n) * g(n)).
也就是说,假设T1(n) = O(n),T2(n) = O(n^2),则T1(n) * T2(n) = O(n^3)。落实到具体的代码上,我们可以把乘法法则看成是嵌套循环,我举个例子给你解释一下。
1 | |
我们单独看cal()函数。假设f()只是一个普通的操作,那第4~6行的时间复杂度就是,T1(n) = O(n)。但f()函数本身不是一个简单的操作,它的时间复杂度是T2(n) = O(n),所以,整个cal()函数的时间复杂度就是,T(n) = T1(n) * T2(n) = O(n*n) = O(n^2)。
我刚刚讲了三种复杂度的分析技巧。不过,你并不用刻意去记忆。实际上,复杂度分析这个东西关键在于“熟练”。你只要多看案例,多分析,就能做到“无招胜有招”。
几种常见时间复杂度实例分析
虽然代码千差万别,但是常见的复杂度量级并不多。我稍微总结了一下,这些复杂度量级几乎涵盖了你今后可以接触的所有代码的复杂度量级。
对于刚罗列的复杂度量级,我们可以粗略地分为两类,多项式量级和非多项式量级。其中,非多项式量级只有两个:O(2^n)和O(n!)。
当数据规模n越来越大时,非多项式量级算法的执行时间会急剧增加,求解问题的执行时间会无限增长。所以,非多项式时间复杂度的算法其实是非常低效的算法。因此,关于NP时间复杂度我就不展开讲了。我们主要来看几种常见的多项式时间复杂度。
1. O(1)
首先你必须明确一个概念,O(1)只是常量级时间复杂度的一种表示方法,并不是指只执行了一行代码。比如这段代码,即便有3行,它的时间复杂度也是O(1),而不是O(3)。
1 | |
我稍微总结一下,只要代码的执行时间不随n的增大而增长,这样代码的时间复杂度我们都记作O(1)。或者说,**一般情况下,只要算法中不存在循环语句、递归语句,即使有成千上万行的代码,其时间复杂度也是Ο(1)**。
2. O(logn)、O(nlogn)
对数阶时间复杂度非常常见,同时也是最难分析的一种时间复杂度。我通过一个例子来说明一下。
1 | |
根据我们前面讲的复杂度分析方法,第三行代码是循环执行次数最多的。所以,我们只要能计算出这行代码被执行了多少次,就能知道整段代码的时间复杂度。
从代码中可以看出,变量i的值从1开始取,每循环一次就乘以2。当大于n时,循环结束。还记得我们高中学过的等比数列吗?实际上,变量i的取值就是一个等比数列。如果我把它一个一个列出来,就应该是这个样子的:
所以,我们只要知道x值是多少,就知道这行代码执行的次数了。通过2 ^ x=n求解x这个问题我们想高中应该就学过了,我就不多说了。$x=\log n$ (以2为底)所以,这段代码的时间复杂度就是:$O(\log n)$(以2为底)
现在,把代码稍微改下,你再看看,这段代码的时间复杂度是多少?
1 | |
根据我刚刚讲的思路,很简单就能看出来,这段代码的时间复杂度为$O(logn)$ (以3为底)。
实际上,不管是以2为底、以3为底,还是以10为底,我们可以把所有对数阶的时间复杂度都记为$O(logn)$(以2为底)。为什么呢,我知道有些人忘了,下面我帮你论证了一下,用对数的换底公式就可以了!
基于我们前面的一个理论:**在采用大O标记复杂度的时候,可以忽略系数,即O(Cf(n)) = O(f(n))**。所以,$O(logn)$ (以2为底) 就等于$O(logn)$ (以3为底)。因此,在对数阶时间复杂度的表示方法里,我们忽略对数的“底”,统一表示为$O(logn)$。
如果你理解了我前面讲的$O(logn)$,那$O(nlogn)$就很容易理解了。还记得我们刚讲的乘法法则吗?如果一段代码的时间复杂度是$O(logn)$,我们循环执行n遍,时间复杂度就是$O(nlogn)$了。而且,$O(nlogn)$也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是$O(nlogn)$。
3.O(m+n)、O(m*n)
我们再来讲一种跟前面都不一样的时间复杂度,代码的复杂度由两个数据的规模来决定。老规矩,先看代码!
1 | |
从代码中可以看出,m和n是表示两个数据规模。我们无法事先评估m和n谁的量级大,所以我们在表示复杂度的时候,就不能简单地利用加法法则,省略掉其中一个。所以,上面代码的时间复杂度就是O(m+n)。
针对这种情况,原来的加法法则就不正确了,我们需要将加法规则改为:T1(m) + T2(n) = O(f(m) + g(n))。但是乘法法则继续有效:T1(m)*T2(n) = O(f(m) * f(n))。
空间复杂度分析
前面,咱们花了很长时间讲大O表示法和时间复杂度分析,理解了前面讲的内容,空间复杂度分析方法学起来就非常简单了
前面我讲过,时间复杂度的全称是渐进时间复杂度,表示算法的执行时间与数据规模之间的增长关系。类比一下,空间复杂度全称就是渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
我还是拿具体的例子来给你说明。(这段代码有点“傻”,一般没人会这么写,我这么写只是为了方便给你解释。)
1 | |
跟时间复杂度分析一样,我们可以看到,第2行代码中,我们申请了一个空间存储变量i,但是它是常量阶的,跟数据规模n没有关系,所以我们可以忽略。第3行申请了一个大小为n的int类型数组,除此之外,剩下的代码都没有占用更多的空间,所以整段代码的空间复杂度就是O(n)。
我们常见的空间复杂度就是O(1)、O(n)、O(n2 ),像O(logn)、O(nlogn)这样的对数阶复杂度平时都用不到。而且,空间复杂度分析比时间复杂度分析要简单很多。所以,对于空间复杂度,掌握刚我说的这些内容已经足够了。
小结
基础复杂度分析的知识到此就讲完了,我们来总结一下。
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系,可以粗略地表示,越高阶复杂度的算法,执行效率越低。常见的复杂度并不多,从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2 )。等你学完整个专栏之后,你就会发现几乎所有的数据结构和算法的复杂度都跑不出这几个。
复杂度分析并不难,关键在于多练。 之后讲后面的内容时,我还会带你详细地分析每一种数据结构和算法的时间、空间复杂度。只要跟着我的思路学习、练习,你很快就能和我一样,每次看到代码的时候,简单的一眼就能看出其复杂度,难的稍微分析一下就能得出答案。
转自《数据结构与算法之美》–王争