KNN

KNN是监督学习中解决分类问题的一种算法，又叫 K-Nearest Neighbor也叫K近邻算法。

它的一个基本思路是：如果一个样本在特征空间中，K个最近邻的样本中的大多数属于某一类型，那么这个样本也划分为这个类型。我们可以结合下图（图源自WIKI）。来进一步了解一下它是如何对样本点进行分类的。

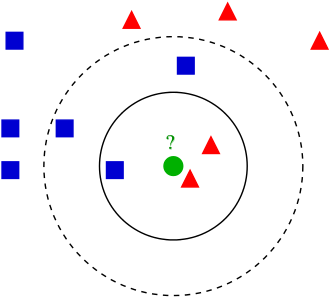
在图示中有两种点，一种蓝色正方形，一种红色三角形，那么现在请问绿色的圆形点会被分到哪一类？

情况一： 假定，找3个(K)离圆点最近的点。是蓝色正方形的概率为1/3；是红色三角形的概率为2/3。那么该点就是红色三角形这一类。

情况二： 假定，找5个(K)离圆点最近的点。是蓝色正方形的概率为3/5；是红色三角形的概率为2/5，那么该点就是蓝色正方形这一类。

由此可见，KNN算法中的K对结果的影响还是蛮大的，因此在训练模型阶段要选取一个合适的K值。

原理

1）计算测试数据和个样本数据之间的距离
2）按照距离的递增关系排序
3）选择距离最小的K个点
4）确定前K个点所在类别的出现频率
5）返回前K个点中出现频率最高的类别作为测试数据的预测分类

代码实现步骤

0.引入依赖

这里引入sklearn里的数据集iris，其中有iris.data（150个样本),iris.target（每个样本的分类）

这里引入skelearn里的train_test_split将iris数据 切分数据集为训练集和测试集

为了判断最终预测结果的好坏，我们使用了sklearn里的accuracy_score函数，它可以方便的计算准确率

import numpy as np
import pandas as pd

from sklearn.datasets import load_iris 
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

1. 数据加载和预处理

加载数据集iris，使用pandas中的DataFrame绘制出表格

iris = load_iris()

df = pd.DataFrame(data = iris.data, columns = iris.feature_names)
df['class'] = iris.target
df['class'] = df['class'].map({0: iris.target_names[0], 1: iris.target_names[1], 2: iris.target_names[2]})
df.head(10)
df.describe()

下面划分训练集和测试集

# x为样本点
x = iris.data
# y为预测分类
y = iris.target.reshape(-1,1)

# 划分训练集和测试集
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=35, stratify=y)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

2. 核心算法实现

# 曼哈顿距离
def l1_distance(a, b):
    return np.sum(np.abs(a-b), axis=1)

# 欧几里得距离
def l2_distance(a, b):
    return np.sqrt( np.sum((a-b) ** 2, axis=1) )

# 分类器实现
class kNN(object):
    # 定义一个初始化方法，__init__ 是类的构造方法
    def __init__(self, n_neighbors = 1, dist_func = l1_distance):
        self.n_neighbors = n_neighbors
        self.dist_func = dist_func
    
    # 训练模型方法
    def fit(self, x, y):
        self.x_train = x
        self.y_train = y
    
    # 模型预测方法
    def predict(self, x):
        # 初始化预测分类数组
        y_pred = np.zeros( (x.shape[0], 1), dtype=self.y_train.dtype )
        
        # 遍历输入的x数据点，取出每一个数据点的序号i和数据x_test
        for i, x_test in enumerate(x):
            # x_test跟所有训练数据计算距离
            distances = self.dist_func(self.x_train, x_test)
            
            # 得到的距离按照由近到远排序，取出索引值
            nn_index = np.argsort(distances)
            
            # 选取最近的k个点，保存它们对应的分类类别
            nn_y = self.y_train[ nn_index[:self.n_neighbors] ].ravel()
            
            # 统计类别中出现频率最高的那个，赋给y_pred[i]
            y_pred[i] = np.argmax( np.bincount(nn_y) )
        
        return y_pred

3. 测试

# 定义一个knn实例
knn = kNN()
# 训练模型
knn.fit(x_train, y_train)

# 保存结果list
result_list = []

# 针对不同的参数选取，做预测
for p in [1, 2]:
    knn.dist_func = l1_distance if p == 1 else l2_distance
    
    # 考虑不同的k取值，步长为2
    for k in range(1, 10, 2):
        knn.n_neighbors = k
        # 传入测试数据，做预测
        y_pred = knn.predict(x_test)
        # 求出预测准确率
        accuracy = accuracy_score(y_test, y_pred)
        result_list.append([k, 'l1_distance' if p == 1 else 'l2_distance', accuracy])
df = pd.DataFrame(result_list, columns=['k', '距离函数', '预测准确率'])
df

最终结果如下图所示：

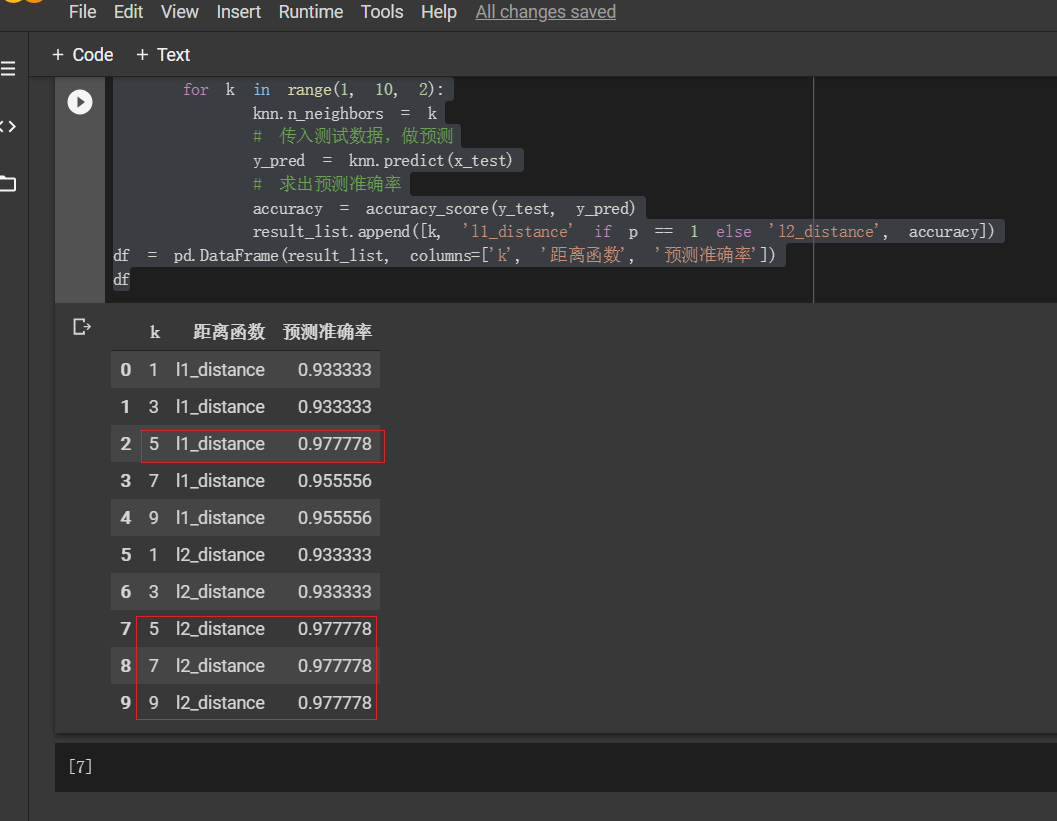
选择欧几里得距离 K=5,7,9和选择曼哈顿距离 k=5 取得的效果最好！