SkipList

本文我们用Java实现跳表的创建

一. 跳表介绍

我们知道单链表的查询时间复杂度为O(n)，那么有没有优化的办法呢？这里介绍一种数据结构，叫跳表，跳表应用十分广泛，比如最熟悉不过的redis，Redis中的有序集合（Sorted Set）就是⽤跳表来实现的。另外Java JUC中也有它的影子，想要了解的可以看下ConcurrentSkipListMap和ConcurrentSkipListSet ，其中底层实现都是使用了跳表。

之前提到如何优化链表的查询速度，想一下把二分查找的思想应用到单链表查找上，会是什么样？下面介绍一种办法，就是在链表上层创建索引，下面用一个图来解释。

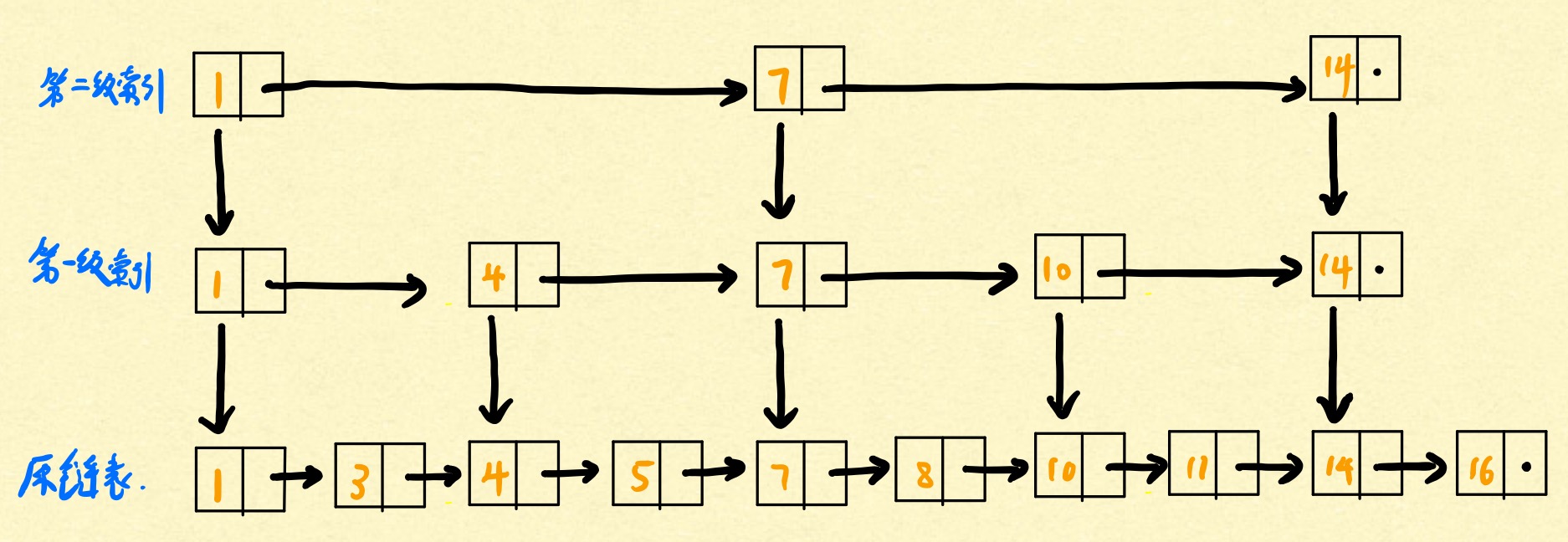
我们在原链表的基础上创建两级索引，比如查询16，如果没有索引，9次命中目标；而使用了2级索引，3次就命中了目标，不难发现这是一种使用空间换区时间的策略。

二.代码说明

1. 基本定义

public class SkipList {

    private Node head = new Node();  // 带头链表
    private int levelCount = 1;

    private class Node {
        private int data = -1;
        private Node forwards[] = new Node[MAX_LEVEL];
        private int maxLevel = 0;

        @Override
        public String toString() {
            StringBuilder builder = new StringBuilder();
            builder.append("{ data: ");
            builder.append(data);
            builder.append("; levels: ");
            builder.append(maxLevel);
            builder.append(" }");

            return builder.toString();
        }
    }
}

• head 是头结点,head.forwards[0]指的是原链表,head.forwards[1]指的是第一级索引,head.forwards[2]指的是第二级索引以此类推
• levelCount 当前构造跳表索引的最大层数值
• Node 是链表

2. 插入实现

动态更新

在插入前需要考虑一个问题，索引的更新问题。如果我们不更新索引，只是单纯的插入节点，会造成索引间节点的值过多，查询速度退化问题。因此这边在插入时需要实时更新索引，一种简单的办法就是把原来的索引删了，重新创建索引。

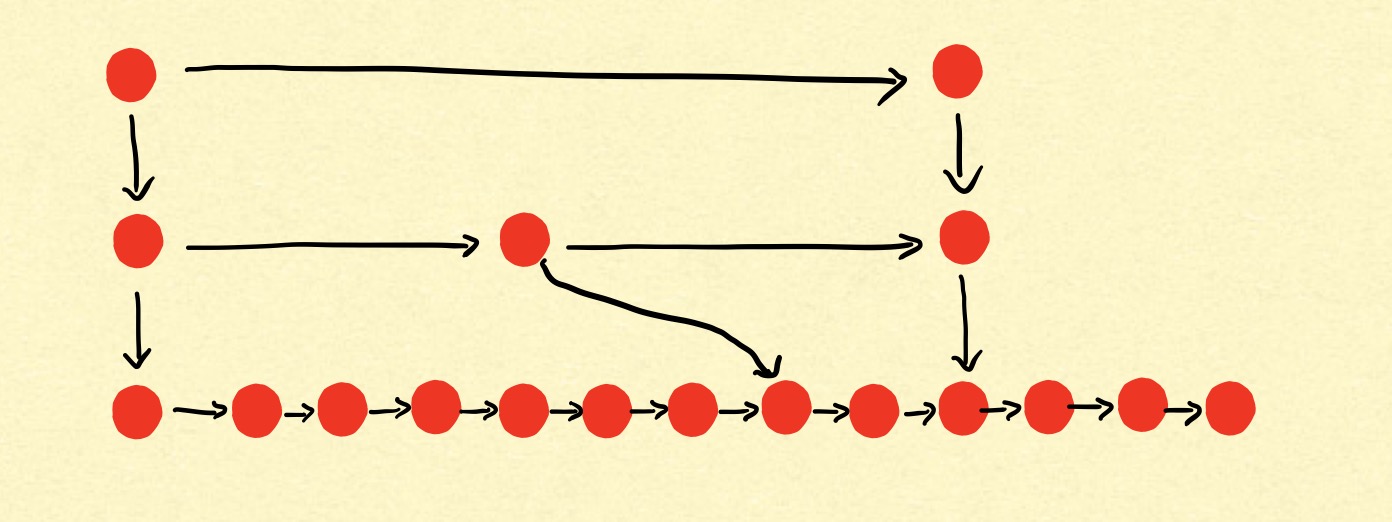
概率算法

我们不难发现原链表中节点个数为n，第一级索引节点个数为n/2，第二级索引节点个数为n/4，第m层索引节点个个数为n/2^m。不难发现，每层的节点个数都是有规律可循的，这里利用概率学推出概率函数randomLevel(),假定给一个值V，就能算出它的层L，通俗一些讲，对于插入的新值V，有50%几率建立一层索引，有25%的几率建立二层索引，有12.5%的概率建立三层索引…

private static final float SKIPLIST_P = 0.5f;
private static final int MAX_LEVEL = 16;

// 理论来讲，一级索引中元素个数应该占原始数据的 50%，二级索引中元素个数占 25%，三级索引12.5% ，一直到最顶层。
// 因为这里每一层的晋升概率是 50%。对于每一个新插入的节点，都需要调用 randomLevel 生成一个合理的层数。
// 该 randomLevel 方法会随机生成 1~MAX_LEVEL 之间的数，且 ：
//        50%的概率返回 1
//        25%的概率返回 2
//      12.5%的概率返回 3 ...
private int randomLevel() {
    int level = 1;

    while (Math.random() < SKIPLIST_P && level < MAX_LEVEL)
        level += 1;
    return level;
}

Redis 的Sorted set也同样使用了类似的算法，详情查看t_zset.c，搜索ZSKIPLIST_P跳转到对应位置有兴趣的可以详细看一下。

代码实现

public void insert(int value) {
    # 获取层
    int level = randomLevel();
    
    # 构造当前节点
    Node newNode = new Node();
    newNode.data = value;
    newNode.maxLevel = level;
    # 辅助数组，下表0代表是原链表，下表1代表是第一级索引，下表2代表第二级索引
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
        update[i] = head;
    }

    // 找当前节点插入的位置。解释：对于索引高度为n的跳表 寻找与插入值紧挨着的最小值，将其放在辅助数组里
    Node p = head;
    for (int i = level - 1; i >= 0; --i) {
        while (p.forwards[i] != null && p.forwards[i].data < value) {
            p = p.forwards[i];
        }
        update[i] = p;
    }

    // 将当前节点插入到每层的链表中的指定位置。
    for (int i = 0; i < level; ++i) {
        newNode.forwards[i] = update[i].forwards[i];
        update[i].forwards[i] = newNode;
    }

    // 更新跳表索引的高度
    if (levelCount < level) levelCount = level;
}

下面方便学习提供源码