BFS

前文了解了如何用深度优先遍历算法去遍历图，本文换一种方式遍历图，广度优先遍历算法（Breath-First Search），下面用Java实现以下它。

一. BFS介绍

BFS它遍历的策略是：对于当前访问的顶点V，依次访问其所有的兄弟节点，直到遍历完为止，再以兄弟节点重复此操作，直到整个图遍历完为止。下面画个图来看看。

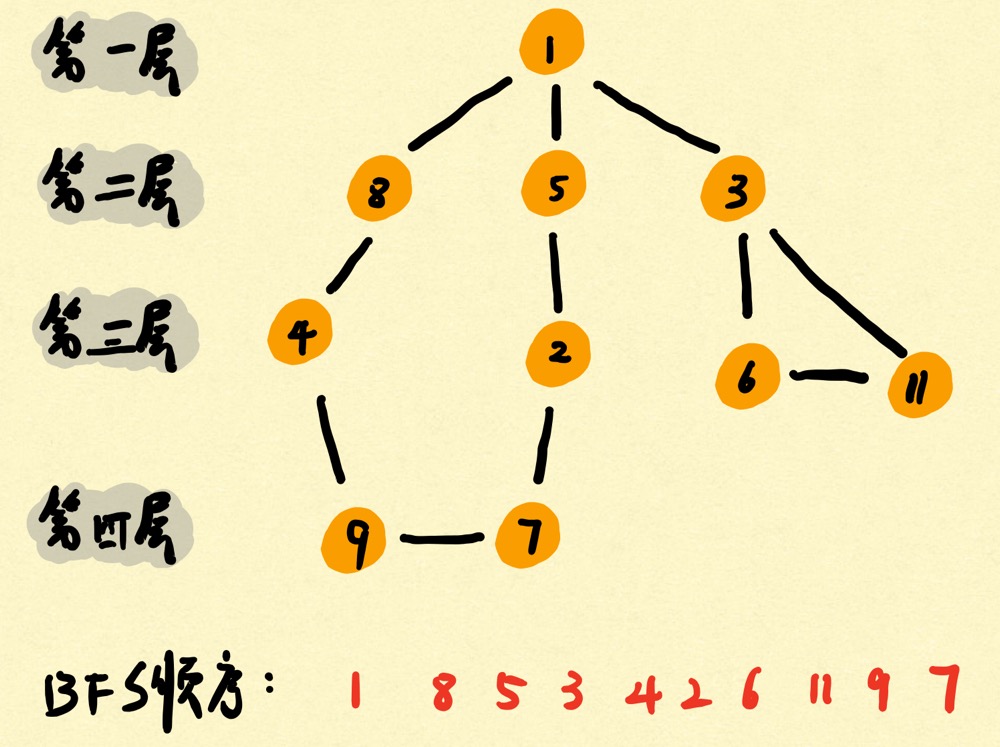
BFS是这样的一个遍历思路，先找到顶点1并输出，找到1的第一个邻接点8并输出，第二个邻接点5输出，第三个顶点3输出，顶点1没有邻接点了；开始以8为顶点输出，8的第一个邻接点4输出，8的第二个邻接点1发现已经访问过了不作处理，顶点8没有邻接点了；开始以5为顶点输出，反复上面操作…那么打印的节点顺序就是1,8,5,3,4,2,6,11,9,7

二.代码说明

我们以邻接矩阵存储实现的图为基础，来实现BFS算法，邻接矩阵有向图实现和无向图实现

首先以分治的思想将大问题划分为小问题，先解决一个顶点的深度搜索问题，在将此拓展到整个图上，也就解决了图的深度搜索问题。

1. 顶点i的深度搜索问题

解决思路

1. 将节点i输出记录已访问，并将节点放到队列T中
2. T不为空开始循环
3. 移除队头节点u
4. 寻找u的邻接点w
5. 如果w存在就循环，否则重复2
6. 如果w没有访问过，就将其放到队列T，输出标记已访问，否则什么都不做
7. 更新w，找u的下一个邻接点，重复5

代码实现

// 广度优先遍历
LinkedList<Integer> queue = new LinkedList<Integer>();//辅助队列
int w; // 第n个邻接点
int u; // 头结点
boolean[] visited = new boolean[n];// 已访问节点

public void bfs(int i) {

    // 输出i记录已访问，加入队列T
    System.out.print(vertexs.get(i) + "->");
    visited[i] = true;
    queue.addLast(i);

    // T不为空就开始循环
    while (!queue.isEmpty()) {
        u = queue.removeFirst();
        // 找到邻接点
        w = firstNeighbor(i);
        while (w != -1) {
            if (!visited[w]) {
                // 找到的邻接点没访问过，就输出记录已访问，加入队列T
                queue.addLast(w);
                System.out.print(vertexs.get(w) + "->");
                visited[w] = true;
            }
            // 寻找下一个邻接点
            w = nextNeighbor(u, w);
        }
    }
}


private int nextNeighbor(int i1, int i2) {

    for (int j = i2 + 1; j < edge[i1].length; j++) {
        if (edge[i1][j] == 1) {
            return j;
        }
    }
    return -1;
}


private int firstNeighbor(int index) {
    for (int i = 0; i < edge[index].length; i++) {
        if (edge[index][i] > 0) {
            return i;
        }
    }
    return -1;
}

2. 图的深度搜索问题

上面我们已经将单个顶点的深度遍历问题解决了，下面只需要把方法套一下就可以了。

public void bfs() {
    // 对于所有的顶点vertexs，依次遍历
    for (int i = 0; i < vertexs.size(); i++) {
        if (!visited[i]) {
            bfs(i);
        }
    }
}

3. 时间复杂度分析

关于有n个顶点m条边的图来说时间复杂度是什么呢？可以考虑这样一个问题，对于最坏情况来讲，从最开始的顶点h，找到最终的顶点e，每一个顶点都要进出一次队列，每一个边都会被访问一次，因此时间复杂度O(n+m)。

对于一个连通图来讲，一般边m的都是大于n-1的，因此时间复杂度通常可以简化为O(m)

方便大家学习，查看源代码