Topological Sort

这里讨论一下拓扑排序，以及怎么检查有向图有没有带环。

DAG介绍

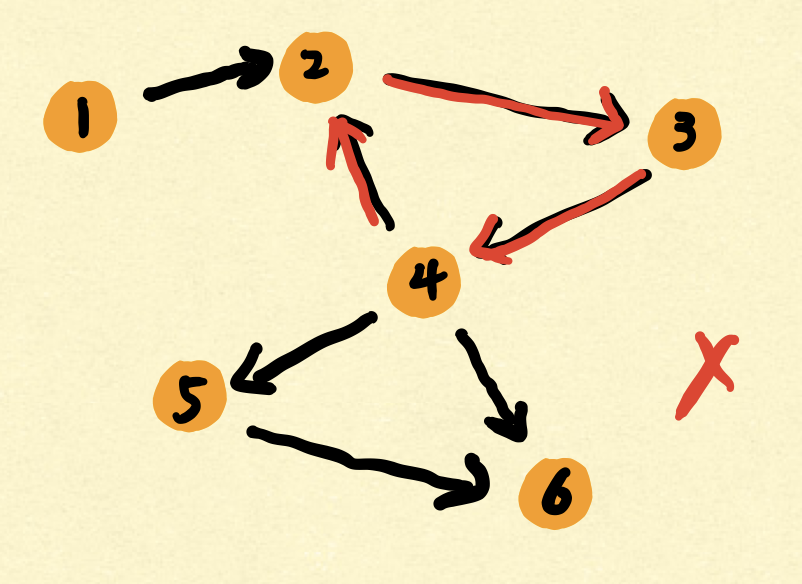
DAG叫有向无环图，他描述了整个连通图中的某个子图不能带有环的，只要有环，就不能称为有向无环图。

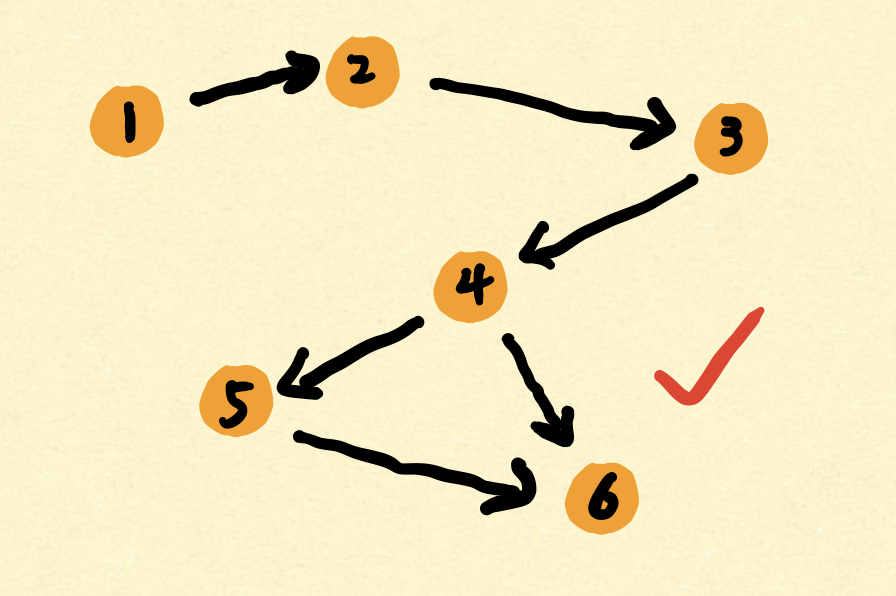
下图是错误的，带环的图。

拓扑排序介绍

拓扑排序该算法在1972年设计编译器时被发明出来，当时的问题是，怎么解决代码编译的依赖问题。因为代码都是有顺序的，例如：C代码文件依赖B代码文件，B依赖A，B依赖D，那在编译时就不能先编译B，得将A和D先编译完了，才能编译B。所以编译的顺序要么是[A,D,B,C]，要么是[D,A,B,C]。拓扑排序可以将图转为顺序表，挨个打印这个表，就是正确的顺序了。

关于拓扑排序的实现有很多办法BFS、DFS、Kahn都可以实现，下面用Kahn实现以一下。

Kahn算法实现

关于代码的实现不复杂下面简单理一下实现思路:

定义数据结构的时候，如果s需要先于t执⾏，那就添加⼀条s指向t的边。所以，如果某个顶点⼊度为0， 也就表示，没有任何顶点必须先于这个顶点执⾏，那么这个顶点就可以执⾏了。

我们先从图中，找出⼀个⼊度为0的顶点，将其输出到拓扑排序的结果序列中（对应代码中就是把它打印出来），并且把这个顶点从图中删除（也就是把这个顶点可达的顶点的⼊度都减1）。我们循环执⾏上⾯的过程，直到所有的顶点都被输出。最后输出的序列，就是满⾜局部依赖关系的拓扑排序。

下面是代码简单思路

下面Java实现拓扑排序（有向图是用邻接表的方式存储）：

• 初始化图顶点的入度
• 将入度为0的顶点放到辅助队列T
• 当T不为空，就取出队列的顶点，并从T中删除
• 把取出的顶点放入队列Q中，并且把这个顶点从图中删除（也就是把这个顶点可达的顶点的⼊度都减1），如果入度为0，将其放到T，等下次循环，否则什么都不做。

关于有向无环图的邻接表实现可以看一下这个源码

//辅助队列T
private Queue<Integer> queue;

public int sort(ListDG listDG){
    ListDG.VNode[] vNodes = listDG.getVNodes();

    int index = 0;
    queue = new LinkedList<Integer>();
    char[] res = new char[vNodes.length];
    int[] ins = new int[vNodes.length];

    // 初始化所有顶点的入度
    for (int i = 0; i < vNodes.length; i++) {
        ListDG.ENode edges = vNodes[i].firstEdge;
        while(edges != null){
            ins[edges.index]++;
            edges = edges.next;
        }
    }

    //将入度为0的顶点放入到队列中
    for (int i = 0; i < ins.length; i++) {
        if(ins[i] == 0)
            queue.add(i);
    }

    while(!queue.isEmpty()){
        int v = queue.remove();
        res[index++] = vNodes[v].data;

        // 获取到所有的边
        ListDG.ENode edges = vNodes[v].firstEdge;
        while(edges != null){
            // 这里入度-1，就当做删除边操作了
            ins[edges.index]--;

            if(ins[edges.index] == 0)
                queue.add(edges.index);

            edges = edges.next;
        }
    }

    if(index != vNodes.length){
        System.out.println("图有环");
        return 1;
    }

    // 遍历T队列
    System.out.print("图的拓扑排序结果为:");
    for (int i = 0; i < res.length; i++) {
        System.out.print(res[i] + "\t");
    }

    return 0;
}

算法时间复杂度

从Kahn代码中可以看出来，每个顶点被访问了⼀次，每个边也都被访问了⼀次，所以，Kahn算法的时间复杂度就是O(V+E)（V表示顶点个数，E表示边的个数）。

图有没有带环

其实检查环的问题。只适用于，已知一个图，检查图中环的场景，看顺序表中的length是不是为顶点的个数就能监测是不是有环，因为它的效率真的是太低了，要处理完整个图才能看到结果。比如场景：已知数据库中的所有顶点的依赖关系了，检查顶点间到底有没有环。这个问题，就需要⽤到拓扑排序算法了。我们把关系从数据库中加载到内存，然后构建成这种有向图数据结构，再利⽤拓扑排序，拿到排序完的顺序表，检查环。

另外一种场景就是，插入一个关系以后，监测是否出现环，这时候再用拓扑排序显然性能有点low，下面介绍一个稍微好点的。举个例子比如下图:

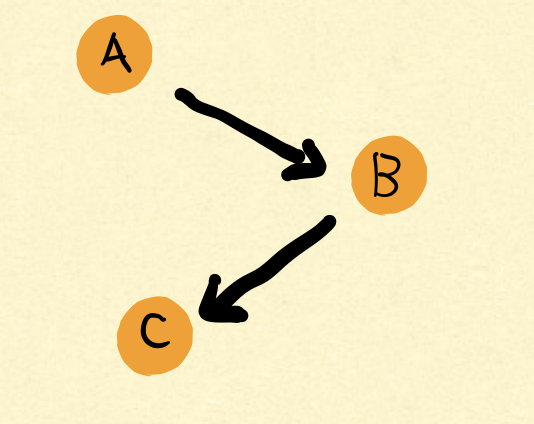
这个时候插入C指向A的边以后，怎么监测带没带环？使用BFS或者DFS遍历顶点，用哈希表记录已访问过的顶点值。

HashSet<Integer> hashTable = new HashSet<>(); // 保存已经访问过的vertex

然后如果放的时候发现哈希表里面已经存在，那就意味着出现环了。

方便折腾的时候参考，源码